
Bit permutations
Back to main page
Comments or questions? E-mail: info@sirrida.de
 Intro
Intro
This is a description of several bit permutation types
as well as some routines performing them.
You can
download
an
implementation of the routines.
In contrast to the routines posted elsewhere most of them act in a
SWAR-like fashion
and hence have an additional parameter which describes the
subword size.
I have also prepared an
online code generator
for practical permutations.
It currently operates only on 32 bit since PHP cannot reliably do more.
There is also the program
calcperm.pas
resp.
calcperm.cpp,
you can compile yourself
which does not have this limitation.
Several routines are presumably published here for the first time
such as a bit-parallel implementation of
compress-flip and expand-flip
which I am very proud of.
Not two weeks after I published the first public version of the bit permutation stuff on http://programming.sirrida.de (setup on 2011-06-01), Intel introduced (published 2011-06-11, proposed for 2013, released about 2013-06) two new instructions for x86 processors named PEXT and PDEP. They have the potential of massively speeding up some (but not all) of the routines. The introduction of these future instructions caused several changes of this site…
On this site I assume that the underlying machine has a word size of a power of 2 using two's complement for integer numbers. For non-conforming systems I have not taken any precautions and thus you should not use the routines on them but with extreme care and exhaustive tests.
The equations on this site are roughly in C syntax in order to avoid multiple description systems. I hope that fans of other programming languages will excuse me.
 Word definitions
Word definitionsHere are some word definition used on this site:
A bit is the smallest piece of information and can contain the boolean values 0 or 1. Alternatively you can associate the truth values false and true.
A number can be seen as an array or group of bits when written in base 2. A group of 8 bits is called a byte or an octet. The bit group the processor can most naturally process is called a word.
Bits are numbered "right" (least significant bit, index 0)
to "left" (most significant bit), i.e.
76543210.
The reason for this numbering is the naming of the
shift operations, i.e.
the
shift right operator >>
should shift to the right side and
the shift left operator <<
should shift to the left side.
This is only a notation issue
and has nothing to do with memory layout
(endian
problem).
For further information you may look up some information in Wikipedia.
bits is the used
word
size.
bits = 2ld_bits.
The bitwise
boolean
operators
act in parallel on an array of
bits,
i.e. on a whole
word.
If they act on a single bit (a boolean value),
they are simply called boolean operators.
Here are the most common ones:
The
not
or inversion operator ~
converts 0 to 1 and vice-versa.
Other names include complement and
negation ¬.
The C operator ! is similar but acts on boolean values.
The
and
operator & becomes
1 if all of its operands are 1,
and 0 otherwise.
This operation is
idempotent,
commutative
and
associative.
Other names include intersection ∧
and conjunction ∩;
the operation generates a subset.
The C operator && is similar but acts on boolean values
and is evaluated with short-circuit evaluation.
The
inclusive or
or simply or operator | becomes
1 if any operand is 1,
and 0 otherwise.
This operation is
idempotent,
commutative
and
associative.
Other names include union ∨ and
disjunction ∪.
The C operator || is similar but acts on boolean values
and is evaluated with short-circuit evaluation.
The
exclusive or,
xor or exor operator ^ becomes
1 if the sum of its operands is odd,
and 0 otherwise (even);
therefore it has the meaning of "odd parity".
When applied to the usual two operands the result can be interpreted in
the verbatim meaning of "exclusive or" as
"either-or", and also as "not equal" or "different".
This operation is
commutative
and
associative.
Other names include symmetric difference Δ and
exclusive disjunction ⊕.
I have also seen >< which is fortunate because
it looks similar to an X (like eXclusive or)
and is also similar to the "not equal" operator <> in Pascal.
Paradoxically there is no corresponding C operator dedicated to boolean values.
| sources | not | and | or | xor | ||
|---|---|---|---|---|---|---|
| a | b | ~a | ~b | a & b | a | b | a ^ b |
| 0 | 0 | 1 | 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 | 1 | 1 | 0 |
d is the parameter describing the direction; it can hold the values left and right.
Here integer numbers are values which are mostly unsigned.
Numbers might be encoded in other bases such as 10
as was done on ancient computers.
Today only base 2 (i.e. bits) is used,
and this is what is crucially needed for all bit operations.
If signed numbers are present,
it is assumed that they are encoded as
two's complement,
e.g. the bit representation of -1 contains only bits with the value 1, i.e. ~0.
This makes sense because it avoids signed zeros and
also avoids special treatment of negative numbers for addition and subtraction.
However the most negative number has no positive counterpart.
Overflows occurring in operations must typically be ignored.
A number is usually stored in a
word.
Hexadecimal numbers (numbers of base 16)
are often prefixed with 0x (C style programming languages)
or $ (Pascal),
or are postfixed by H (Assembler).
ld_bits is the
binary logarithm (log2) of
bits (the used
word
size).
bits = 2ld_bits.
Similar to
shift
the rotate operation moves bits in the denoted direction
but feeds the bits back in on the other side.
Although most processors support these operations directly
unfortunately most programming languages have no intrinsic support therefor.
A rotation by n is equal to n rotations by 1.
These operations are cyclic with a cycle length equal to the
word
/
subword
size.
The rotate right operator moves bits to the right.
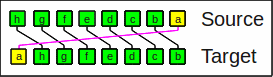
Rotate right by 1
The rotate left operator moves bits to the left.
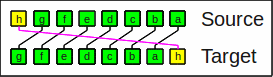
Rotate left by 1
It is the inverse of the rotate right operator.
The shift operators move bits in the denoted direction.
A shift by n is equal to n shifts by 1.
On this site n is assumed to be
≥ 0
and <
bits.
A shift by ≥
bits
is undefined by the C/C++ standard.
For almost all processors
either
n is masked by 31, 63, or 255 (i.e. 5, 6, or 8 bits)
or
there is no instruction with a variable amount of shifting.
Thus shifting x by n =
bits
usually yields either x (i.e. shifted by 0)
or the natural result
which is 0 (or -1 for an arithmetic shift of a negative number).
x >> n
(i.e. x shifted right by n)
is equal to
x / 2n
rounded toward negative infinity.
There are two different shift right operators:
The logical shift right operator
shifts in zeros (division of unsigned numbers by powers of 2).
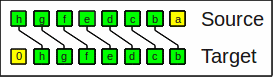
Logical shift right by 1
The arithmetic shift right operator
duplicates the highest bit
(division of signed numbers by powers of 2).
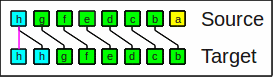
Arithmetic shift right by 1
On this site only the logical shift right operator >>
is used.
x << n
(i.e. x shifted left by n)
is equal to
x * 2n;
overflows (superfluous bits) are discarded.
The operation is the same for signed and unsigned numbers.
Shift left by 1
On this site a subword denotes a part of a word and is a bit string/array/group consisting of 1<<sw bits, e.g. one bit (sw=0), nibble (4 bit, sw=2) or byte (8 bit, sw=3).
Subwords are always aligned to their natural boundaries, e.g. bytes always start at a bit position divisible by 8; see bit numbering above.
Some of the algorithms also work (or can be modified to work) with arbitrary large subwords and/or even with different sized subwords within words.
sw is the parameter describing the granularity; it is the binary logarithm (log2) of the number of bits of one subword.
A word is essentially the same as a
subword
but is the amount of information the processor can naturally process.
It can e.g. hold an
integer number.
In the examples given on this page I chose a
working size
of 8
bit
and in the
source files
you can currently choose between 8, 16, 32, 64,
and possibly 128 bit.
It is not difficult to modify most of the routines to act on
SIMD,
registers as well,
especially when sw is constant.
Almost all contemporary processors store
integer numbers
in binary as
two's complement,
using a
word size
of a power of 2.
Very old processors used e.g. 12 or
36
bit.
Also, some embedded processors might use e.g. 24 bit.
Some kinds of bit processing such as the ones on the
Beneš network
make little sense or more effort
for word sizes of non-powers of 2.
 Source files
Source files
The source files of the
test programs,
testperm.c
resp.
testperm.pas
and their include files
contain an implementation of most routines discussed here.
The include files are perm_bas.* and perm_b#.*
where # is 8, 16, 32, 64, or possibly 128.
See also the
list of function descriptions.
I have also prepared some x86 32 and 64 bit assembler routines
demonstrating the usage of the instructions
PEXT and PDEP:
perm_32.asm
and
perm_64.asm.
There is also a small collection of
macros for bitwise shifts on xmm registers
in
xshift.asm.
Finally there are the sources in calcperm.pas. resp. calcperm.cpp permutation code generator which works similar to the online version.
You can download these files by right-clicking on the links and selecting "Save as". For convenience all sources are packed into one ZIP archive.
 Comments on the test programs
Comments on the test programs
The test programs
contains an implementation and a simple test
of most of the routines discussed here.
For convenience I have prepared versions in C / C++ and Pascal.
There is also a list of function descriptions.
The test programs should be compiled to a console application
in order to get the debug output.
Overflow-checking should be turned off.
Be sure that the
shift right
operator
(>> resp. shr)
shifts logical, i.e. shifts in zeros.
For optimum readability, adaptability and portability I have not used
compound assignment operators such as ^= or += and
liberally used parentheses;
I have also resisted to use classes.
I have used the C++ style // comments for better readability than
the usual /* … */.
I have formatted the sources according to the
Ratliff style
which has proven to be optimally readable.
DidIMentionThatIHateCamelCaps?!
I_think_that_names_with_underscores_are_much_better_readable.
The code should be compilable with any modern C compiler such as
GCC.
You might need to adapt the include statements
and the debugging output functions.
See also my general comments on
C / C++.
The Pascal version is essentially the same as the one in C.
It should be compilable with a modern Pascal compiler like
Delphi
(aka Turbo/Borland Pascal, commercial),
Free Pascal
(free), and even
GNU Pascal
(free).
If you face problems with your Pascal compiler,
you might need to change the const parameters
to var or value parameters.
Also the // comments might need to be changed into the
usual (* … *) ones.
The type-casted constants, especially lo_bit,
also can be problematic and
might needed to be replaced by the typecased values in place,
i.e. e.g. lo_bit by t_bits(lo_bit).
Procedures which are passed as parameters might need to be declared FAR.
When you address all those mentioned obstacles,
even the ancient compilers
Borland Pascal and Delphi-1 (16 bit) can be utilized.
See also my general comments on
Pascal.
For a real application in a program you should take care that all
generator and usage routines presented in the test programs
will be fully unrolled, i.e. contain no loops,
and that for a word size of 32 bit or less
all constants from the arrays are realized as manifest constants.
On x86 processors bigger values can only
be used as a memory operand or
assigned as constants to a register.
This means that the routines with a a loop containing a variable
loop count should have a switch statement for the small number of values
sw
can have.
Fully unrolling shuffle and unshuffle is sumptuous due to the many cases sw1 and sw2 can have combined; I am not sure whether this is the best way to go.
I have given some clues in the programs as ALL CAPS.
By the way: It might happen that the unrolled routines are slower than the ones with loops. This depends e.g. on the actual parameter sw, how often the routine is called, the memory bandwidth, first level cache size, and the instruction decoding speed of the processor.
Especially when the loops are not unrolled,
it might make sense to do some optimizations such as loop-inductions.
For example
for (i=a; i<=b; ++i) {
s=1<<i;
…
}
can typically be converted to
s=1<<a;
for (i=a; i<=b; ++i) {
…
s=s<<1;
}
As hinted in the comments for tr_bfly
it makes sense to change it into a class and
encapsulate the generator and usage routines
as private in this class
and finally add public methods which use the object (instance of this class)
as a means to cache the generated configuration.
The usage of a cache is also part of my proposal of a
hardware implementation
thereof for usage in a processor.
 Generalized bit reversal
Generalized bit reversalThis function (general_reverse_bits) is capable of swapping subwords of the next bigger subword (twice the size); for every subword size it can be specified whether all such pairs shall be swapped or left in place.
The extra parameter k can be seen as a bit array where each set bit
means that all corresponding
subwords
of size 1<<sw
shall be swapped.
Examples (for a word size of 32 bit):
If you arrange the bits in matrix form you can do mirror operations on it, e.g. arrange 32 bits on a 4×4 matrix of 2 bit entries:
For other sizes (with edge sizes of a power of 2) and dimensions (hyperrectangles) similar things apply.
The function is the inverse of itself. The necessary swapping stages can be performed in any order.
You will find the definition and implementation thereof also in
the excellent book
Hacker's Delight,
(chapter 7.1, "Generalized Bit Reversal").
I have presented this useful function here only for completeness.
This operation is a bit index manipulation and performs any bit complement permutation where k is the value to be xor-ed with the bit index, and is therefore also called the xor permutation which is a subset of bit permute/complement permutations.
For a diagram of a hardware implementation thereof see
butterfly network.
Every steering bit corresponds to one complete butterfly stage.
The next described function prim_swap is a generalization.
 Swap by primitives
Swap by primitives
Also this function
(prim_swap)
is capable of swapping subwords of the
next bigger subword (twice the size);
in contrast to
general_reverse_bits
for any such pair it can be specified whether it shall be
swapped or left in place.
The order of the swapping stages matters.
For convenience the two main orders
can be selected by the highest bit.
This corresponds to selecting whether the
butterfly
operation (1) or its inverse (0) is used.
For detailed description you may download
Jörg Arndt's
excellent free e-book
Matters Computational
(chapter 1.29.1, "A restricted method")
which is also available as a real paper book.
There you will also find an
implementation;
however only a rather slow version is presented.
I have created a bit-parallel version thereof which does not
loop over all the bits.
I give credit to
Jörg Arndt
for the idea to this useful function.
According to him,
the function can e.g. perform the
Gray
permutation and its inverse.
For a diagram of a hardware implementation thereof see
butterfly network.
Every steering bit corresponds to the boxed parts of a butterfly stage.
 Shuffle and unshuffle
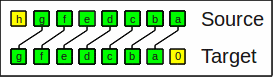
Shuffle and unshuffleThe (outer perfect) shuffle (shuffle) operation defined in Hacker's Delight, (chapter 7.2, "Shuffling Bits"), interlaces the bits of the 2 subwords of a word twice the size. It it also known as bit zip or interlace operation. You can e.g. use it to calculate Morton numbers for 2 dimensions.
For e.g. a word size of 8 the bits
dcbaDCBA are shuffled into
dDcCbBaA:
The shuffle operation
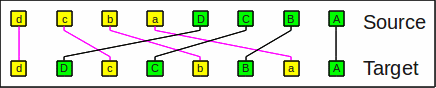
The operation can also be seen as a
transposition
of a rectangle (ordered right to left and bottom to top):
The shuffle operation as a transposition
The inverse operation is
(outer perfect) unshuffle
(unshuffle)
which is also known as bit unzip or uninterlace operation.
dDcCbBaA is unshuffled into
dcbaDCBA:
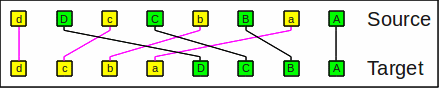
The unshuffle operation
My versions of these routines extend the operation
in that they can act on arbitrary sized subwords,
i.e. the sizes of the entities to be shuffled
as well as
the range where the shuffling occurs
can be specified.
You can for example shuffle the bits in all bytes, or the nibbles in all words.
Similarly applying these extended operations sw2-sw1 times
yield same result as the source.
Shuffle and unshuffle are a special case of the sheep-and-goats operation resp. its inverse.
By the way:
The extended [un]shuffle routines can be emulated with
compress and expand
which act on subwords
whose log2 of its size is at least
sw2.
It does not matter whether the _left or the _right
variants are used
as long as an compress is followed by the corresponding
expand.
Since the merged bits are disjunct you can replace the operator
|
by
+
or
^.
a_bfly_mask is an array containing special masks
also needed for the implementation e.g. of a
butterfly
step;
you will find examples for 8, 16, 32, 64, and possibly 128 bit in the
test programs.
For all d1 and d2 the following holds:
shuffle(x,sw1,sw2)
= expand(compress(x,a_bfly_mask[sw2-1],d1),a_bfly_mask[sw1],d1)
| expand(compress(x,~a_bfly_mask[sw2-1],d2),~a_bfly_mask[sw1],d2)
unshuffle(x,sw1,sw2)
= expand(compress(x,a_bfly_mask[sw1],d1),a_bfly_mask[sw2-1],d1)
| expand(compress(x,~a_bfly_mask[sw1],d2),~a_bfly_mask[sw2-1],d2)
This makes it trivially possible to use PEXT and PDEP for the implementation using d1=d2=right.
For the simple versions of [un]shuffle (i.e. working on full word size: sw=ld_bits) things get simpler: Only two compress or two expand operations followed by an | operation are necessary.
Applying these operations sw times
yield the same value as the source.
This becomes evident when you look at the corresponding
bit index manipulation:
The bit index is rotated
left (shuffle)
resp.
right (unshuffle)
by 1.
Talking of rotation:
I have also prepared the function
bit_index_ror
which can rotate a subfield of
the bit index by any amount,
thus enabling an easy calculation of the powers of [un]shuffle
(i.e. [un]shuffle multiple times):
unshuffle_power
and
shuffle_power.
These operations can be seen as
matrix transpositions
and are needed for an emulation of the
omega-flip network
to have the steering bits at the preferred position.
 Compress and expand
Compress and expandThe compress operation (compress) gathers all denoted bits on one side and zeros out the rest. It it also known as generalized extract, bit gather or bit pack operation.
As an example of compress_right, the bit string
hgfedcba and a mask
10011010 results in
0000hedb.
As you can see, the bits h,e,d,b are crammed to the right
and the remaining spaces are filled with 0:
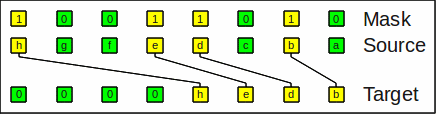
Example for compress_right
The expand operation (expand) is the inverse and distributes the bits to the denoted places; remaining bits are zeroed out as well. It is also known as bit deposit, bit scatter or bit unpack operation.
With expand_right the bit string
hgfedcba and a mask
10011010 results in
d00cb0a0:
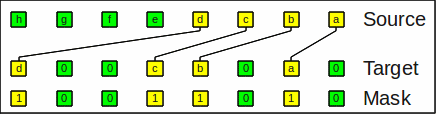
Example for expand_right
Here is an example for compress_left:
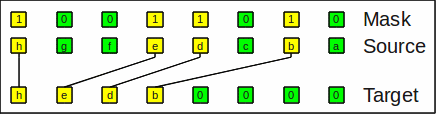
Example for compress_left
Here is an example for expand_left:
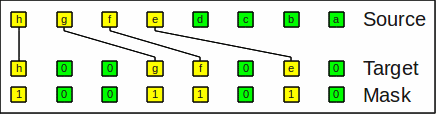
Example for expand_left
My versions of the compress/expand routines extend the ones of Hacker's Delight (chapter 7.4, "Compress, or Generalized Extract"), to be acting on all subwords of arbitrary size.
PEXT and PDEP are hardware implementations of the simple versions where the subword size equals the word size.
Using both
PEXT and PDEP
also these extended versions can be performed.
Unfortunately additional masks must be provided.
For extended compress the bits are first collected to one side
and then must be distributed back to the side of the
subwords.
Essentially the needed bits must be stuffed to one end of each
subword.
For extended expand the things are similar.
It appears that this mask compression functionality is a by-product of
the mask generators for compress and expand
but was never used before;
also, for all d and sw
the following holds:
compress_mask(m,sw,d) = compress(m,m,sw,d)
For all d, d1 and sw ≤ sw1 (which is always true for sw1=5 [6] for a word size of 32 [64] bit as needed for usage of PEXT and PDEP!) the following holds:
compress(x,m,sw,d) = expand(compress(x,m,sw1,d),compress_mask(m,sw,d),sw1,d1)
expand(x,m,sw,d) = expand(compress(x,compress_mask(m,sw,d),sw1,d),m,sw1,d1)
For usage of PEXT and PDEP you must use d=right.
For the special cases shuffle and unshuffle this problem appears twice as described in Sheep-and-goats operation but the masks are constants (only dependent on sw).
 Butterfly network
Butterfly network
Butterfly networks
are great for permuting stuff.
A butterfly network
(bfly)
consists of multiple different butterfly stages.
Each stage
(butterfly)
is an arrangement of
multiplexers
where the corresponding bits of the two
subwords of a
subword
can be swapped individually.
You can arrange the working bits on a
hypercube
of edge length 2.
The corresponding partner bits
can now be found on connected axes
where each axis corresponds to one butterfly stage
(i.e. the X axis corresponds to stage 0, Y to 1, and so on):
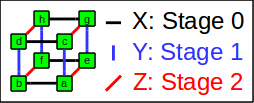
Hypercube of dimension 3
Corresponding partner bits have a distance of 1 << stage number.
See also the chapter where the
hypercube is revisited.
For the inverse butterfly network (ibfly) the order of the stages are reversed. When fed with the same configuration it simply undoes the permutation of the butterfly network.
For a word size of n bit each stage needs n/2 steering bits. This amount of configuration is normally too much to be specified directly, so it makes sense to offer some methods to generate them.
To make a bit-parallel implementation work sufficiently fast in software
I distributed the steering bits into a steering mask in a way that
the mask bits with the lower (right) index are used and the others are zero;
I call this an expanded mask.
A compressed mask has all the steering bits being crammed to the right.
If necessary you can expand a compressed mask.
In these diagrams the data bits (square boxes) are treated from top to bottom;
These boxes are input and output of the stages.
The blue bullets on the right are the butterfly configuration.
For our uses we need a circuitry which can be configured to
pass through or cross two connections.
A
multiplexer
(often abbreviated as MUX)
is a circuitry which switches multiple inputs to one output.
Multiplexers are symbolized by trapezia.
We need pairs of them.
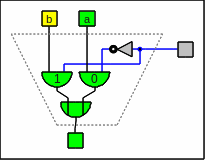
A multiplexer as circuitry
A demultiplexer does the inverse and
switches one input to multiple outputs.
In order to utilize demultiplexers for our uses
we need to combine the outputs of two of them with an
or
gate
…
and we effectively get the same circuitry.
Therefore this is the only place on this page
where demultiplexers are mentioned.
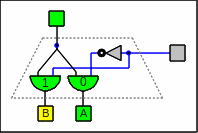
A demultiplexer as circuitry
Using pairs of multiplexer
0 (black connector) means that the bits go straight through,
and 1 (magenta connector) means that they have to be swapped.
In other words:
A steering line with 0 lets the red boxes select the left line and
the green boxes the right one
and for a 1 the boxes choose the other ones:
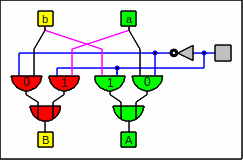
A pair of multiplexers as circuitry
in my preferred mixture of
styles,
mostly of out-dated
DIN 40700
(before 1976)
[easiest to draw and to recognize]
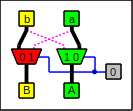
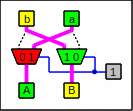
Feeding a pair of multiplexers with 0 and 1
In the software emulation the positions of the green multiplexers are
where in the mask the steering bits are located,
and the steering bits for the red positions are zero.
This is the butterfly network for 8 bit:
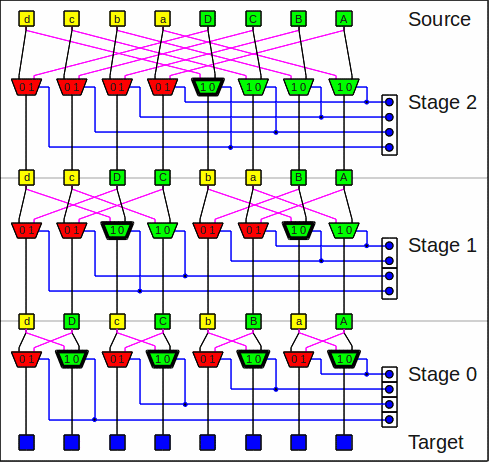
The butterfly network
And this is the inverse butterfly network,
note that only the stage order differs:
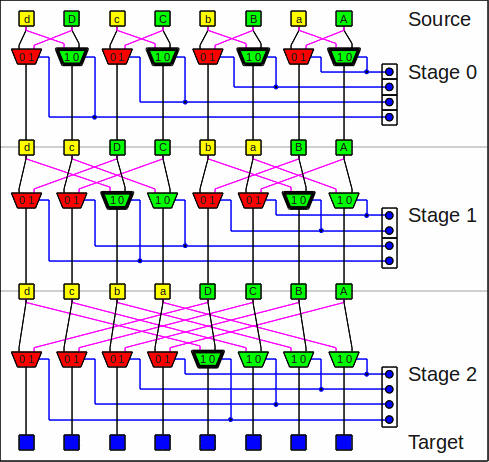
The inverse butterfly network
Among other things the [inverse] butterfly network can perform the following:
Unfortunately the [un]shuffle operations and most of their powers can not be performed with an [inverse] butterfly network.
For generalized bit reversal each bit of its configuration must be copied to all steering bits of the corresponding stage, i.e. bit i corresponds stage i. Since this function is its own inverse it does not matter which butterfly network is used.
For swap by primitives the bits of its configuration mask whose place is denoted with the green multiplexers with a thick frame must be copied to all steering bits of the corresponding group denoted with a box around the butterfly configuration bits. When the most significant bit is 1 the butterfly network is used, for 0 it is the inverse network.
It happens that the code (loop body) for shuffle and unshuffle is the same as for the butterfly operations, albeit with non-conforming masks: The operations themselves cannot be performed on a butterfly network. You will find a proof thereof in the Internet.
You can find numerous articles on the web from Yedidya Hilewitz and Ruby B. Lee about butterfly operations and an implementation in hardware, e.g. here or here.
 Beneš network
Beneš network
A butterfly network (stages a) concatenated with
an inverse butterfly network (stages b)
is called a
Beneš network
and is capable of creating any permutation.
Even with the reversed concatenation order
this type of network is called a Beneš network.
Effectively the stage order is irrelevant,
provided that the front-end has the inverse order of the back-end.
When creating a fixed permutation,
the reordering often saves one stage, i.e. the corresponding mask is zero.
The two innermost stages of a Beneš network (stages 0a and 0b)
can obviously be replaced by one (stage 0)
by
xor-ing
the corresponding steering bits together:
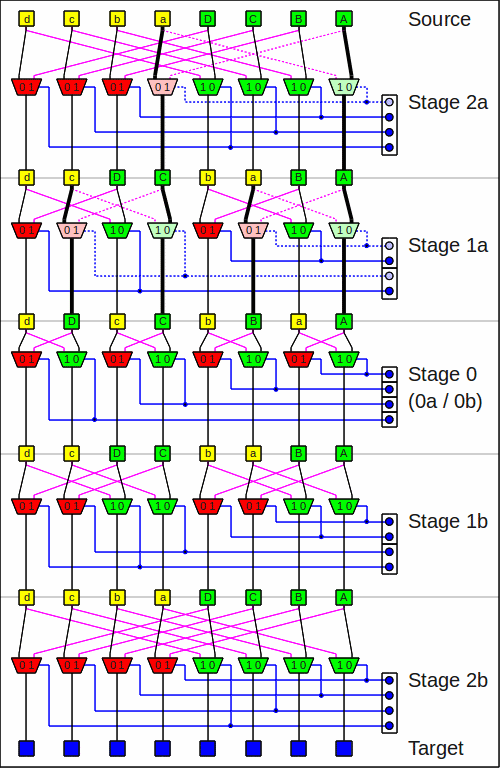
The Beneš network
Using earlier work of D. Slepian, A. M. Duguid and J. Le Corre independently discovered this network class in 1959. Beneš wrote several articles in the 1960's about networks in the Bell System Technical Journal and made the network popular.
I have prepared the routine
gen_benes
which can generate a configuration for a Beneš network
from a given array of indexes
and two routines
(benes_fwd and
benes_bwd)
to use this configuration.
See
Bitwise tricks and techniques,
(Donald E. Knuth,
"The art of computer programming,
vol. 4, pre-fascicle 1a",
"bit permutation in general",
page 13 ff).
The construction of the configuration recurses
from the outer to the inner stages.
At start all input bits and also all output belong to a set.
On each level the bits of a set
are routed from the input set to one of two subsets
and from the subsets back to the output set.
The subsets are the sets of the next level.
Since for the first inspected unassigned input of a set
the multiplexer gets "do not swap",
the corresponding configuration bit will become 0.
For the innermost input stage (stage 0a) this means
that all source multiplexers will become "do not swap"
and therefore the whole configuration for that stage is zero.
In the image of the Beneš network above
these (for my implementation) superfluous multiplexers
and configuration bits are the very bright ones
with the mandatory connections drawn fat and the unused ones dotted.
Also the innermost input stage (stage 0a) is left out;
this was also noted above as being obvious.
A hardware implementation can thus save some multiplexers.
This is what it takes to simplify a Beneš network into a
Waksman network
(Abraham Waksman,
"A Permutation Network", January 1968,
Journal of the Association for Computing Machinery,
vol. 15 #1, pages 159-163).
The
parity
of a
permutation
can be
even
or
odd
and describes whether
the number of swaps necessary to perform the permutation
can be divided by 2 or not.
Since each pair of multiplexers can either
swap (steering bit = 1)
or route through (steering bit = 0),
the parity of a permutation
simply is the parity of the number of steering bits
of the Beneš network with the value 1.
To ease the calculation you can
xor together all steering masks
and calculate the parity of this intermediate result
by deciding whether the sum of its bits is even or odd.
 Rotate operations
Rotate operationsIt is possible to perform rotate operations with a butterfly operation and also the inverse butterfly operation, even if acting on subwords. Now we have a bit-parallel implementation for the rotate operations:
With these routines it is possible to emulate AMD's new XOP instructions VPROTx (x=B/W/D/Q).
As an example of frol with
sw=2 (nibble, 4 bit)
and a rotate count of 1
(performed on the inverse butterfly network),
the bit string
hgfedcba results in
gfehcbad.
The subwords dcba and hgfe
are both rotated left by 1.
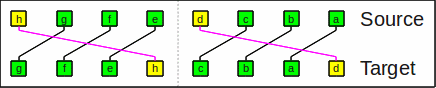
Example of frol by 1
As an example of vror with
sw=2 (nibble, 4 bit)
(performed on the butterfly network),
the bit string
hgfedcba and a "mask"
xx01xx10 results in
ehgfbadc.
The subwords are rotated independently:
dcba is rotated right by 2
and hgfe by 1.
Unused bits of the mask (x) are ignored.
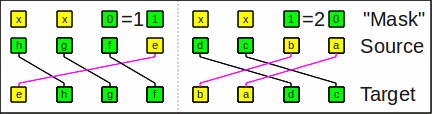
Example of vror
At least the fixed version can be evaluated directly (fror / frol / frot) much faster than via a butterfly network, but who knows… At least it is possible.
 Sheep-and-goats operation
Sheep-and-goats operationThe sheep-and-goats operation, also known as SAG, GRP or centrifuge combines compress_left with the mask inverted with compress_right:
sag(x,m,sw) = compress_left(x,~m,sw) | compress_right(x,m,sw)
Since the merged bits are disjunct you can replace the operator | by + or ^.
By the way: Hacker's Delight's version defines sag with an inverted mask.
As an example of SAG, the bit string
hgfedcba and a mask
10011010 results in
gfcahedb:
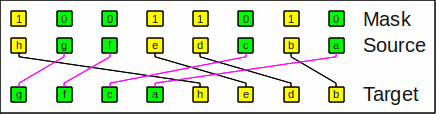
Example for sheep-and-goats
The inverse operation inv_sag (UNGRP) simply undoes it:
inv_sag(x,m,sw) = expand_left(x,~m,sw) | expand_right(x,m,sw)
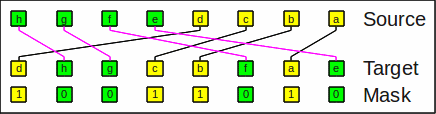
Example for inverse sheep-and-goats
Both of these operations are very versatile but unfortunately quite "expensive" and can not be performed on a butterfly network.
The shuffle operation is an important special case of SAG.
See also PEXT and PDEP for a partial hardware implementation.
I have sketched Knuth's algorithm to use SAG to perform arbitrary permutations in at most sw steps; Lee's algorithm is often even better.
 Compress-flip and expand-flip
Compress-flip and expand-flip
The expensive
sheep-and-goats operation
generally cannot be performed on a butterfly network;
interestingly however,
a variant thereof can
which gathers the denoted bits on one end in order,
but also the remaining ones mirrored on the other end.
I call this operation compress-flip
(compress_flip)
and its inverse expand-flip
(expand_flip).
The operations are also known as gather-flip resp. scatter-flip.
As an example of compress_right_flip, the bit string
hgfedcba and a mask
10011010 results in
acfghedb:
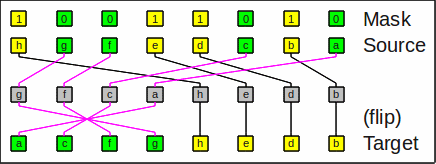
Example for compress_right_flip
The gray intermediate value
(which would be the
sheep-and-goats operation)
is never realized and
is presented here only to better visualize the effect.
The marked bits are gathered at the right end
and the remaining ones are flipped and come to the left.
The inverse operation expand_right_flip simply undoes it,
i.e. transforms acfghedb
back to hgfedcba
when given the same mask.
Here is an example for expand_right_flip:
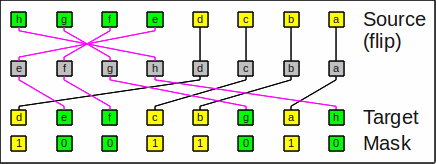
Example for expand_right_flip
Here is an example for compress_left_flip:
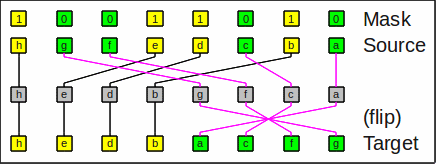
Example for compress_left_flip
Here is an example for expand_left_flip:

Example for expand_left_flip
The compress operation can trivially be emulated by compress-flip:
compress_right(x,m,sw) = compress_right_flip(x&m,m,sw)
compress_left(x,m,sw) = compress_left_flip(x&m,m,sw)
Similarly expand can trivially be emulated by expand-flip:
expand_right(x,m,sw) = expand_right_flip(x,m,sw)&m
expand_left(x,m,sw) = expand_left_flip(x,m,sw)&m
It took me some weeks to figure out how to calculate the butterfly configuration
in an efficient bit-parallel fashion.
You will notice some similarities to the generator routines of
compress and expand.
When fully optimized as described in the
Comments on the test programs,
the setup routine gets quite fast.
The "flip" routines are more versatile, however the usage routines of compress and expand are almost twice as fast as a butterfly operation; also, the masks are more often zero. For fixed operations a zero mask allows for elimination of the corresponding stage.
Hilewitz and Lee describe a hardware implementation thereof and mention the flip operations.
Donald E. Knuth mentions "gather-flip" and writes that
"gather-flip … turns out to be more useful and easier to implement.
Any permutation of 2d bits is achievable by using either
[sheep-and-goats and gather-flip] operation, at most d times".
All these authors make no real use of the "flip" part of the instruction, although this additional functionality can become handy sometimes.
 Knuth's algorithm for SAG/GRP/gather-flip
Knuth's algorithm for SAG/GRP/gather-flip
Here is Knuth's algorithm for using
SAG
for
an arbitrary permutation
(answer 73):
Start with moving all bits with an odd target index (bit 0 is set) to the left;
also order the target indexes accordingly.
In the next step move according to where bit 1 in the target index is set;
repeat until all index bits are treated this way.
On each step half of the bits in the mask is set.
Since every such step represents a
stable sort
of one index bit,
the goal of sorting the target indexes is reached.
Example:
12605743 =>
15732604 =>
73261504 =>
76543210
This shifting is a
SAG operation
on the target bits
as well as on the diagonally mirrored array of bit indexes.
This is also mentioned in
Hacker's Delight,
(chapter 7.5/7.7, "General Permutations, Sheep and Goats Operation").
When this same algorithm is applied to
compress_right_flip,
the sort is obviously not stable because of the "flip";
instead the index bits are sorted into
Gray code
order.
Example:
12605743 => (bit 0)
37512604 => (bit 1)
62735104 => (bit 2)
45762310.
To correct this,
all target indexes
must first be replaced by their Gray code:
Replace: 76543210
=> 45762310 (Gray code).
Example:
12605743 => (Gray code)
13507462 => (bit 0)
75310462 => (bit 1)
26375104 => (bit 2)
45762310.
Obviously similar algorithms exist for
compress_left_flip
and the inverses UNGRP and expand_flip.
 Lee's algorithm (merge lists)
Lee's algorithm (merge lists)
Donatas Radomskis <radomskis.donatas@gmail.com>
brought to my attention that
Ruby B. Lee, Zhijie Shi, Xiao Yang
("Efficient permutation instructions for fast software cryptography",
chapter 3.2)
describe an even better approach using SAG.
Since SAG is invertible, inverse SAG can also be used.
Here is my interpretation and attempt to make it clear.
Assuming the given bit indexes refer target indexes,
we want to e.g. perform the following permutation:
37560421 =>
76543210
We want to sort the indexes
and to note the necessary commands on each step.
The main idea is to split the index list into
ordered partial lists
and to merge pairs of them on each step.
After ceil(ld(n)) steps (maximally) we are finished
because each step halves the number of partial lists.
For odd numbers of partial lists we simply add empty ones.
Using the example from above we get 4 partial lists (no empty one needed):
3, 75 / 60, 421
Now we separate the 4 partial list into the left and the right half.
Afterwards we pairwise merge the left lists with the right ones.
3, 60 => 630 (101)
75, 421 => 75421 (00111)
Starting with the lowest index, one by one fetching the next lowest,
we write down a 0 for a left index and 1 for a right one,
and create a SAG mask this way.
As usual we are starting from the right end.
Afterwards the new partial lists and partial masks are concatenated:
630, 75421
101, 00111
As we see, now the indexes (lists are concatenated)
walk towards the desired order.
The resulting mask can be used for a reverse SAG (aka UnGRP) command
which performs exactly the operation for the partial lists,
and does not intermix the new partial lists.
We could now repeat all this,
but using the combined partial lists suffices.
In our example the final step follows:
630, 75421 => 76543210 (10110110)
All in all these are the resulting commands:
UnGRP 2$10100111
UnGRP 2$10110110
Needless to say, we can possibly improve the result by
trying to prepend or append simple commands such as
ROL or BSWAP and
also trying to use SAG/GRP instead of their reverse operations.
In all cases this approach is at least as good as Knuth's.
It should be possible to adapt this algorithms to use the
flip operations,
inherited instead of SAG.
I leave it as an exercise to the interested reader.
 Omega-flip network
Omega-flip network
Omega and flip networks are funny variants of the
butterfly network.
You need the same number of stages for both network types.
The most interesting feature is that in contrast to butterfly stages
all omega stages
(omega)
are equal;
also all flip stages
(flip)
are equal,
so a hardware solution is quite easy,
especially when the stages are used recurrently.
Unfortunately however
a software emulation is quite expensive on most processors.
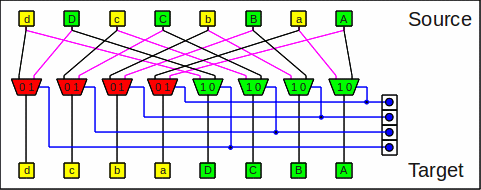
Here is one stage of the omega network:
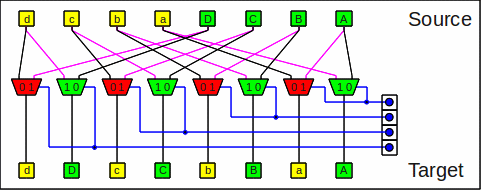
One stage of the omega network
An omega operation is the same as a
shuffle
operation
followed by a
a butterfly step of stage number 0 (called an exchange step):
One omega stage as shuffle+butterfly
This is why these networks are also called shuffle exchange networks.
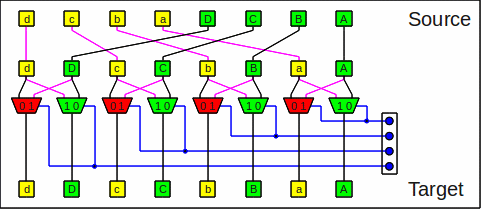
An omega operation is also the same as
a butterfly step at maximum stage number (sw-1)
followed by a
shuffle
operation,
even if it does not look like this at first sight:
One omega stage as butterfly+shuffle
The omega diagrams imply different mask layouts;
for easier handling I prefer the steering bits to be at the positions
as seen in
the lowest one (butterfly+shuffle) and in
the flip diagrams below (compressed masks, see below).
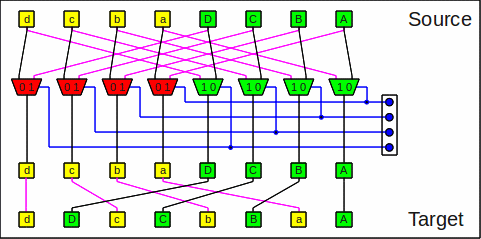
Here is one stage of the flip network:
One stage of the flip network
A flip operation is the same as an
unshuffle
operation
followed by a butterfly step at maximum stage number
(sw-1):
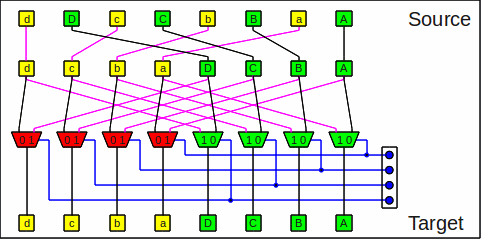
One flip stage as unshuffle+butterfly
For every given configuration the flip operation is the inverse of the omega operation and vice-versa.
An omega-flip network is an omega network
followed by a flip network (or vice-versa).
This is similar to a butterfly network followed by the inverse
being a
Beneš network.
An omega network is isomorphic to a
butterfly network,
and
a flip network is isomorphic to an inverse butterfly network.
Hence an omega-flip network is isomorphic to a
Beneš network
and therefore is also capable of performing any permutation.
To translate the configuration from one network type to the other,
only some shuffling is necessary.
When compressed masks are expanded
to the usual places for the
[inverse] butterfly network
(green trapezoids in the diagram)
and [un]shuffled stage number times
for the omega resp. flip operation,
both network types have the same result.
A compressed mask has all relevant steering bits crammed to the right.
A butterfly stage needs expanded masks for fast simulation.
For more information on omega-flip see numerous articles from Ruby B. Lee and others.
 Bit index manipulations
Bit index manipulations
Some of the mentioned bit permutations can alternatively be
described as operations on the bit indexes.
The bit index manipulation function simply maps the bit indexes.
The allowed bit index range is 0 to x-1
where x is the
word
size in bit.
As an example, for a word size of 32 bit
the indexes 0…31 are mapped to 0…31,
and the index itself has 5 bit.
A bit index function is reversible
if and only if
every index of the valid range is hit exactly once.
Every reversible bit index function
is equivalent to
a bit permutation
and vice-versa.
See also
Hacker's Delight,
(chapter 7.6/7.8, "Rearrangements and Index Transformations")
or
Matters Computational
(chapter 2, "Permutations and their operations").
The bit operations relate to the bit index operations
in a similar way like
* relates to +
or
x relates to log2(x).
Do you remember
slide rules?
As an example a
rotate
left
by 1
adds 1 to each bit index.
Here are some examples of bit permutations and the corresponding reversible bit index functions:
| Bit permutation | Bit index operation |
|---|---|
| Rotate left | The amount to be rotated left is added to the bit index. |
| Rotate right | The amount to be rotated right is subtracted from the bit index. |
| Generalized bit reversal |
Some index bits are inverted, e.g. bits 0, 1, and 4:
43210
=>
43210
The bit index is xor-ed with the parameter k of general_reverse_bits. These are bit complement permutations. |
| Transpose bit hyperrectangles |
The index bits are permuted, e.g.
43210
=>
24301
These are bit-permute permutations; special cases below. For an example see the image "The shuffle operation as a transposition". |
| Shuffle | The bit index is rotated left by 1: 43210 => 32104 |
| Unshuffle | The bit index is rotated right by 1: 43210 => 04321 |
| shuffle_power | The bit index is rotated left by rot. |
| unshuffle_power | The bit index is rotated right by rot. |
If a bit permutation shall occur only
within
subwords
of size 1<<sw,
only the lower sw index bits are affected
and the other index bits remain constant.
In other words:
Operations are performed
modulo
the needed
subword
size.
If a bit permutation shall only mix complete subwords of size 1<<sw, the lower sw index bits remain constant and the other index bits are affected.
It happens that some special bit index operations can be implemented with very little effort. In particular there is a set of very small and fast loop-less auxiliary routines which get especially fast if they are completely inlined with all index parameters being constants. They
These procedures span a small but very powerful subset
of bit index manipulations
called bit-permute/complement permutations (BPC permutations),
also known as dimension permutations.
This class of permutations was defined 1980 by
David Nassimi and Sartaj Sahni
in
"An optimal routing algorithm for mesh-connected parallel computers"
(Journal of ACM 27/1).
Implementing a given permutation by applying these procedure
is about as fast as a
[inverse] butterfly network
operation.
You need at most n of such operations for any BPC permutation of n index bits
where at most n-1 of them are
bit_index_swap or bit_index_swap_complement.
The subclass of bit-permute permutations (without complementing)
are also known as
rational permutations
and their effect can be seen as
transpositions
of n-dimensional
hyperrectangles
also known as orthotopes or
rectangular parallelepipeds
whose edge lengths are powers of 2.
You need at most n-1 bit_index_swap operations
for any bit-permute permutation of n index bits.
Similarly the complement permutations (xor-permutations)
performed by
generalized bit reversal
can be seen as mirror operations on hyperrectangles.
You need at most n bit_index_complement operations
for any complement permutation of n index bits.
Here are some other examples of what you can do with BPC permutations. You can perform
I found the procedures (in ARM assembler) in the ARM System Developer's Guide, (chapter 7.6.2, "Bit Permutations"), and I am quite sure that this is not the only place where these routines can be found.
 Hypercube revisited
Hypercube revisited
The simplest non-trivial hypercube is a square.
Let us assume we have 4 bits (dcba) grouped as follows:
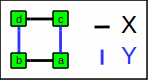
Square / simple hypercube
| Bit | X | Y |
|---|---|---|
| a | 0 | 0 |
| b | 0 | 1 |
| c | 1 | 0 |
| d | 1 | 1 |
Apart from denoting the axes and butterfly stage numbers,
X and Y function as bit index indexes.
For simplicity let us assume that Y>X; otherwise we exchange X and Y.
The corresponding swaps shift the bits by x=1<<X and y=1<<Y.
As in the chapter about the
butterfly network
the bit masks use the lowest possible positions (1)
and the corresponding swap partners (o) lie to the left.
A swap mask and its corresponding shifted swap mask must be disjunct
for the bit permutation primitive
bit_permute_step
to make sense and to work correctly.
These are all permutations of dcba:
| Perm | Mask | Shift | Bfly | BPC | Move | Description |
|---|---|---|---|---|---|---|
| dcba | 0000 | * | * | 10 | 0 | Identity; no operation |
| cdba | o100 | x | X | . | 2 | Swap single pair; exchange X where Y=1 |
| dbca | 0o10 | y-x | . | 01 | 2 | Swap single pair; exchange X and Y axis |
| bdca | . | . | . | . | 3 | Exchange three bits cyclically |
| cbda | . | . | . | . | 3 | Exchange three bits cyclically |
| bcda | o010 | y | Y | . | 2 | Swap single pair; exchange Y where X=1 |
| dcab | 00o1 | x | X | . | 2 | Swap single pair; exchange X where Y=0 |
| cdab | o1o1 | x | X | 10 | 4 | Swap two pairs; complement X |
| dacb | . | . | . | . | 3 | Exchange three bits cyclically |
| adcb | . | . | . | . | 4 | Exchange all four bits in form of "8" |
| cadb | . | . | . | 01 | . | Rotate by 90° CCW |
| acdb | . | . | . | . | . | Exchange three bits cyclically |
| dbac | . | . | . | . | 3 | Exchange three bits cyclically |
| bdac | . | . | . | 01 | . | Rotate by 90° CW |
| dabc | 0o01 | y | Y | . | 2 | Swap single pair; exchange Y where X=0 |
| adbc | . | . | . | . | . | Exchange three bits cyclically |
| badc | oo11 | y | Y | 10 | 4 | Swap two pairs; complement Y |
| abdc | . | . | . | . | . | Exchange all four bits in form of "∞" |
| cbad | . | . | . | . | 4 | Exchange all four bits in form of "8" |
| bcad | . | . | . | . | . | Exchange three bits cyclically |
| cabd | . | . | . | . | . | Exchange three bits cyclically |
| acbd | o001 | x+y | . | 01 | 2 | Swap single pair; exchange and complement X and Y |
| bacd | . | . | . | . | . | Exchange all four bits in form of "∞" |
| abcd | . | . | . | 10 | . | Swap two pairs; rotate 180° |
| Perm | The resulting bit permutation |
| Mask | The necessary mask |
| Shift | The necessary shift |
| Bfly | The butterfly stage |
| BPC | The BPC permutation index vector |
| Move | Special move operation if Y=X+1; see bottom of chapter; shown is the number of affected bits |
| Description | A short description of the permutation |
As you can see
a single usage of the permutation primitive
bit_permute_step
can do all described primitive operations:
A
butterfly
butterfly step and/or one of the
BPC primitives.
Interestingly at most 2 usages of the permutation primitive
bit_permute_step
are necessary for any of the permutations of 4 bit.
I wonder how it is for higher dimensions
and whether there has been some research on that.
Now it is time to make a "real" thing of this discussion about just 4 bits. The needed extended masks can easily be calculated by combining the values of a_bfly_mask with and/or/xor/not. Let mx=a_bfly_mask[X] and my=a_bfly_mask[Y]. Here is the mask replacement table:
| Mask | Extended mask |
|---|---|
| 0001 | mx & my |
| 0010 | ~mx & my |
| 0011 | my |
| 0100 | mx & ~my |
| 0101 | mx |
Example: We want to calculate the permutation dbca (bit_index_swap) for j=X=2 and k=Y=4 for 32 bit:
| x | = 1<<2 | = 4 |
| y | = 1<<4 | = 16 |
| mx | = a_bfly_mask[2] | = 0x0f0f0f0f |
| my | = a_bfly_mask[4] | = 0x0000ffff |
| shift | = y-x | = 12 |
| mask | = ~mx & my | = 0x0000f0f0 |
Hey presto: All the magic stuff can be calculated!
For the special case of Y=X+1 we additionally can
exploit the fact that that x=y-x.
If we move all bits, we need to calculate
((x&m1)<<L) | ((x&m2)>>R):
| Perm | m1 | L | m2 | R |
|---|---|---|---|---|
| adcb | 0001 | x+y | 1110 | x |
| cbad | 0111 | x | 1000 | x+y |
If we move a subset, we need to calculate (x&m0) | ((x&m1)<<L) | ((x&m2)>>R):
| Perm | m0 | m1 | L | m2 | R |
|---|---|---|---|---|---|
| bdca | 0001 | 0010 | y | 1100 | x |
| cbda | 0001 | 0110 | x | 1000 | y |
| dacb | 1000 | 0001 | y | 0110 | x |
| dbac | 1000 | 0011 | x | 0100 | y |
The masks must obviously extended like above.
The last formula is capable of emulating the
permutation primitive
but needs far more parameters.
Therefore
I omitted the permutations from the tables which are already covered by the
permutation primitive.
The natural extension seems to be
bit group moving.
For higher dimensions of the hypercube much more is possible but the things get too complicated to be treated in general here.
 Bit group moving
Bit group moving
It is possible to extract bit groups needing
the same amount of shifting or rotating.
All groups are masked and shifted, and finally combined.
This is ugly and inelegant but can be quite fast,
amazingly often beating the alternatives,
provided that there are not too many such groups.
The worst case however is as horrible as moving bit by bit
as for almost each bit one group is needed.
Keep in mind that for each group one mask is needed.
bit_permute_step
is a special case which needs only
one mask and one shift count parameter
instead of two each.
It is obviously possible to cascade this method.
Unfortunately I have no clue how to do this optimally.
I am quite sure that if the cascading is done properly,
this method will often be the best.
 Shift by multiplication
Shift by multiplication
Multiplication hardware has become amazingly fast.
Since a multiplication can be seen as a bunch of shift and addition operations,
similar to
Bit group moving
bits can also be shifted by a multiplication.
If the factor contains more than one bit
we can create copies of source bits on different locations.
As an example a factor of 3 effectively creates a copy of each masked source bit
one place left to it.
I assume that masks and factors are chosen in such a way that
no addition produces a carry,
at least no carry which might trash a relevant bit.
Some multiplications can be replaced by faster replacements
such as combinations of SHL, ADD, SUB, and LEA on x86.
If the result is masked once more, we can replace some bit group moves.
A carry-less multiplication
such as the newer x86 instruction
PCLMULQDQ
would be a better replacement just because no carries are generated.
Unfortunately this instruction only acts on SSE registers,
and is painfully slow (at least in early implementations).
To some extent this method is similar to
PEXT and/or PDEP.
This an other similar approaches can be advantageously used for bitboards in
chess programming.
 PEXT and PDEP
PEXT and PDEP
This chapter might be slightly off-topic
but is nevertheless interesting and useful…
In the document
319433-011
(June 2011)
the *_right variants of
compress and expand
are introduced (proposed for 2013, released about 2013-06) by
Intel
as "Haswell New Instructions"
for x86 processors
and are named
PEXT (parallel bits extract)
and
PDEP (parallel bits deposit)
(in the BMI2 instruction set).
They act on 32 and 64 bit "general purpose" registers,
albeit without the possibility to specify
subword
sizes
(it equals the word size;
sw is always maximum, i.e. 5 resp. 6).
You can use the free assembler
NASM
to assemble these instructions if you use a version of 2011-07-08 or later, see
snapshots.
The
Intel Software Development Emulator
≥ 4.29 (dated 2011-07-01)
is capable of emulating these instructions
if you have hardware which does not natively execute them.
I have prepared some assembler code for
emulating some of the functions of this article.
In contrast to the routines of the
test programs
sw is always 5 resp. 6 here.
To reflect this
I modified the function's names
in that I appended the missing parameter values.
The routines shall demonstrate
the usage of PEXT and PDEP by some examples.
As you will see, the instruction
POPCNT
(nr_1bits)
which simply counts the 1 bits
is a good friend of these instructions
and is typically available for
Intel processors since SSE4.2
and
AMD processors since SSE4a.
For the 32 bit routines I assume that only eax, edx and ecx are freely usable registers, and also these registers are in this order used for parameters. The result is placed in eax. This arrangement conforms to the register calling convention of Delphi. You will find the routines in perm_32.asm.
For the 64 bit routines I assume the parameters in rcx, rdx, r8, r9 and the result in rax. This conforms to the (IMHO stupid) 64 bit Windows calling convention; however in contrast to the Windows convention I have not put any extra stuff into the routines (such as setting up stack frames, what for?). You will find the routines for 32 and 64 bit math in perm_64.asm.
For other operating systems or calling conventions you will need to adapt the routines; this should be easy.
 Gather/scatter
Gather/scatter
Assuming
PEXT and PDEP
present,
similar to
BIT group moving
we can collect (extract/compress) groups of bits
having ascending target indexes with PEXT
and redistribute (expand) these bits with PDEP into their final position.
These groups are finally combined.
If the masks used for collecting and redistributing are the same
or can be made the same by shifting,
we can replace this whole step by simple masking and shifting.
For contiguous groups of bits we can replace PEXT and/or PDEP
with simple masking and shifting.
When we detect that we scatter and gather the same pattern,
we can optimize this by moving all other bits with the same distance
for the same "price" as well as we do in
bit group moving.
The worst case is about the same as in
BIT group moving.
 Speeding up permutations
Speeding up permutationsFor all optimization tips I am assuming that we have to permute large buffers in the same (usually fixed) way such as in image operations:
Promoting the mentioned permutations to SSE is straight forward
for subword sizes up to 8 bytes.
Shifting longer subword sizes up to 128 bit
can be emulated with not too much effort,
see [v]xpsrldq and [v]xpslldq in
xshift.asm.
The SSSE3 instruction PSHUFB can be utilized for
an arbitrary shuffling of bytes.
All
BPC permutations
on 128 bit can be done with only
3 BPC bit shuffling steps and one PSHUFB instruction
or even less.
Also, PSHUFB can be
utilized as a miniature lookup table
(16 elements);
two of such instructions acting on masked subsets
can be combined (using POR) to e.g.
mirror all bits in every byte.
AMD's new XOP instruction VPPERM can do everything PSHUFB does but can do much more such as drawing from 2 sources and mirroring bits. Unfortunately Intel has not (yet?) copied the XOP instruction set.
For AVX2 processing with a subword size of 256 bit we may need to cross lanes.
Here VPERMD and VPERMQ come handy, but we may also need explicit masking.
For additional speedup
2 or even a few more calculations can easily be done in parallel
by interleaving the instruction streams.
This is a win because most processors are
superscalar
nowadays.
The masks are very often the same for all streams and
need only be loaded once in this case.
This is especially a gain for the SSE/AVX2 variants
because of the missing immediate values
which must be replaced by memory accesses.
AVX2's VPBROADCAST instructions might also help in this case.
Very recent x86 processors even support even more
relevant instructions, i.e. AVX-512.
A chapter about this is really missing.
 Alternatives
AlternativesThere are alternative ways to perform bit permutations.
The most obvious alternative is to extract one bit after the other
and insert it into the right place of the result (or vice versa).
In assembler you may use the carry flag.
These types of methods are by far the slowest you can get.
Bit group moving
is typically a much better generalization thereof.
According to first tests the methods with PEXT and PDEP, i.e. gather/scatter and arbitrary permutations with SAG, will be quite fast since both instructions have a latency of 3 cycles and are fully pipelined, i.e. they a reciprocal throughput of 1 cycle. It might be that these instructions will become even faster in subsequent generations.
It is possible to do few permutations with special instructions like ror, rol, and BSWAP.
Another idea is to build a lookup table. For up to about 16 bit this might be feasible but for more it is not since the needed space is simply too large; e.g. for a direct lookup of 32 bit the needed table space is 232*4 byte = 16 GiB.
A workaround
is to split the input into some parts, apply lookup tables,
and combine the looked up results with an operation like
or,
xor,
and,
or add.
For 32 bit one might use e.g. a split up into 4 tables of 256 entries each;
this costs "only" 4*256*4 byte = 4
KiB.
Evidently the more parts are used
the slower it will perform while using less memory:
A space-time trade-off.
The tables must be (pre-) calculated which adds to the costs.
An operation done by splitting up into 4 tables of 256 entries each
is typically faster than a
butterfly
operation for 32 bit
but it needs quite a lot of table space which is used in a random fashion
and thus might fill up or even trash the first level cache.
The timing is largely depending on the used processor,
the processor load
(especially while
hyper-threading),
and the actual usage of the routine.
Keep in mind that
first level data caches are quite small,
typically only some
kibibytes.
When operating on a larger working size, say 64 bit,
the table lookup method
is still valid but costs twice the time and 4 times the space
whereas the version using shifts and masks
costs only 6/5 of the time and 2*6/5 of the space
making it much more attractive.
An easy extension of the lookup version to SSE or AVX2 is not possible,
albeit AVX2's proposed gather instruction might help.
On the other hand this table lookup method allows for much more functionality
than permutations;
for example bits can be replicated, inverted or set to a fixed value.
Depending on the combining operation, other functions are possible as well.
The lookup version might be fast and flexible but
is IMHO plain boring while the
"magic"
shifting variants are interesting and funny.
 Comments on the permutation code generator
Comments on the permutation code generatorIn my online permutation code generator I check for any bit permute/complement permutation (5!*25=3840 combinations) as well as for any stage ordering (5!=120 combinations) of a reordered Beneš network. The reordering very often saves one stage, i.e. the corresponding mask is zero.
Furthermore I analyze the cost of bit group moving. This method can be deactivated.
Finally I optionally challenge the methods gather/scatter and sheep and goats utilizing PEXT and PDEP. According to timing tables published by Agner Fog these instructions cost 3 cyles latency (and throughput 1) each and hence are slower than one AND and a connected SHL/SHR/ROL instruction, so I optimize to masking and shifting if possible.
The cycle calculation is not perfect and might not correctly reflect the real timing since the superscalar nature of modern processors can not be simulated easily and also heavily depends on the used processor.
I have no clue how to find the very best sequence of permutation macros. If you know of an algorithm which runs in acceptable time, please let me know.
There is also a version of the permutation code generator in Pascal,
calcperm.pas
resp. C++,
calcperm.cpp.
In contrast to the online permutation code generator
the Pascal / C++ version also features
some additional permutation approaches and
an optional optimization which prefixes and/or postfixes most permutations
with ROL (only once)
and/or BSWAP (at most 3 times:
once first,
once last, and
once between ROL and the main permutation).
These options massively slows down the computation.
The slow down becomes relevant for bits > 32
since the whole calculation for the remaining permutation is
done for every combination with ROL and/or BSWAP as described above
(up to about 16*bits times).
If you do not want to spend that much time, you should switch off the
ROL optimization completely with the parameter "/opt_rol=0".
The ROL optimization
for the most time consuming permutations (BPC and Benes)
is switched off as default (i.e. "/opt_rol_ex=0").
Talking of parameter:
The file calcperm.ini shows all parameters
but the actual indexes.
Do not expect the
online permutation code generator
to include this feature,
since PHP is too slow for such escapades, even for 32 bits.
You can adapt the functionality by changing
the bit depth in the sources (different include file)
or modifying
calcperm.ini.
The output is not necessarily the same as in the online version.
The online (PHP) version is based on an older version of the Pascal source.
 Summary
SummaryIf you need a fixed permutation, you may consult the online permutation code generator or compile and use the source version calcperm.pas resp. calcperm.cpp.
If you need a permutation many times in your program,
determine its type and - if applicable -
use a special generator and its evaluators.
Special cases include
[inverse] butterfly networks
and perhaps
BPC permutations
whereas in the general case you can employ the
Beneš network
or even the
bit group moving
method.
The methods
gather/scatter
and
sheep and goats
only make sense when you have real hardware which can execute
PEXT and PDEP.
Also, a runtime dispatching between several methods might be fortunate.
 Index
Index
Here is a list of some key words
and where you find them.
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z