
Hashing
Back to main page
This is a
Comments or questions? E-mail: info@sirrida.de
 Hashing
Hashing
A
hash function
is essentially a mapping function which transforms a
given key to a hash value
which is a member of a relatively small number range
0…nr_slots-1.
In case you wonder why I have often abbreviated "number" to "nr":
I could have also chosen "num" or even "cnt",
however the often used "no" is misleading and thus unsuitable.
A hash container uses a hash value as an index to
an array of subcontainers.
Therefore each subcontainer
contains only entries with the same hash value.
A good hash function generates
each of the nr_slots possible hash values with about equal probability.
The idea is "divide and conquer",
i.e. you can locate an element faster in a smaller container.
Given that the hash function
is evaluated fast enough and
produces sufficiently different hash values,
even a simple linear scan through the selected subcontainer suffices,
although other strategies can be used as well such as
binary trees or even using yet another hash container.
For now we choose a linear list.
Obviously the method degenerates to a linear scan through all
elements if nr_slots=1
or if the hash function always returns the same value.
However for an evenly distributing hash function
and when nr_slots is given a value of about the number of elements,
we can locate an element with only one or two comparisons on average;
also, we can very quickly prove whether an element is absent.
Decreasing the load factor α
(which is the number of elements divided by nr_slots)
makes the subcontainer smaller and thus the lookup faster
but increases the memory consumption.
In the examples of this chapter
the hash function takes the first character in ASCII
which is masked with 7
using the
and
operator, i.e. the lowest 3 bits are extracted.
The most straight forward implementation of a hashing container
goes like this:
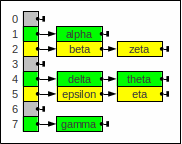
Chained hashing
This container is easily filled and queried at runtime.
However when the lists grow too large we need to
increase nr_slots and to rehash (rebuild)
the complete container.
An alternative to using subcontainers is
to put the elements directly into the array
thereby circumventing an indirection.
In case of a collision, i.e. the needed slot is already used,
we can simply use the (circular) next free slot.
To prove the absence of an element we need to scan the
container until we find a hole
or we are at the starting point again.
Obviously it is necessary
to enlarge nr_slots at least to the number of elements
because otherwise there is no free slot.
To achieve reasonable speed,
the number of elements should be a good deal smaller than nr_slots,
i.e. the load factor α should be well below 1 (100%).
There are some methods to choose the next free slot.
A
linear scan
is cache-friendly
but often the performance is a disaster when
the number of elements approach nr_slots.
Slightly better is to let the increment increase as in
quadratic probing.
Yet other methods use a second hash function such as in
double hashing
or
cuckoo hashing.
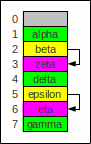
Hashing with probing
Here the magenta elements could not be placed in the correct place
and were therefore placed in the next free slot.
Empty slots are denoted gray.
When the table finally gets full,
obviously the last inserted element will be placed on the last free space.
In this example this is "theta"
which needs 5 (!) comparisons to be found with linear probing:
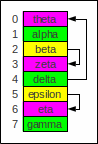
Hashing with probing (full)
To prove the absence of any element we need to scan the
whole container
because of the way too high load factor 1
and thus the absence of empty slots.
Chained hashing
does not have this problem…
A container using linked lists has obviously a lot of pointers.
For a static container (i.e. no additions and no deletions necessary)
there is a compact representation which gets rid of all linkage pointers
but needs nr_slots+1 pointers or better yet indexes:
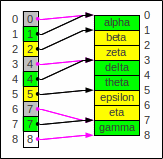
Static hashing compacted
The number of elements of a subcontainer is given by the difference
of the index and the next one.
The gray indexes are equal to the next index.
The arrows in the image point to the top of each element
in order to better show the nature of the indexes.
If we have static container with a perfect hash function (all subcontainers have at most one element), things get simpler, particularly, we can get rid of the loop for checking.
We can omit all next pointers
but we still have to use pointers in the main container:
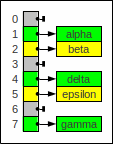
Perfect hashing without next pointers
We can put the elements directly into the array.
Empty slots can be marked as such
either by a special flag or by supplying any element with
a different hash value:

Perfect hashing in-place
Similar to above
we can use a compact representation using indexes.
Empty slots refer to dummy elements:
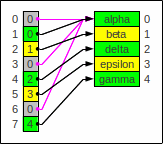
Perfect hashing compacted with dummy entries
 Static hashing of integers
Static hashing of integers
Let us now consider the case that we have got a constant set
of unsigned integer numbers of the type t_base.
These could be e.g.
the cases of a switch/case statement
or
the result of an unmasked (raw) hash function
of constant objects such as strings.
The main methods to narrow these numbers x
to the needed number of slots nr_slots,
i.e. 0…nr_slots-1 are
The constants m, s and d are must be chosen such that the result is < nr_slots. If each of the nr_slots slots shall be used, masking and shifting imply that nr_slots is a power of 2; the modulo function and division imply no restriction on nr_slots but are much slower. As a matter of fact, for unsigned numbers masking / shifting are special cases of modulo / division.
In order to enhance distribution,
we can modify ("scramble") the numbers before the narrowing.
Obviously this only makes sense if things get faster,
therefore the scrambling must be very fast.
Here are some very cheap operations which scramble and narrow
the raw number x (c is a constant);
I assume that any overflows are ignored:
Especially effective is the last one,
since most modern CPUs can multiply quite fast (about 4 cycles)
and we have lots of constants to choose from.
By supplying suitable constants,
we can often significantly reduce the collision lists and
in many cases even achieve perfect hashing
which typically amortizes the scrambling effort.
For example, using 32 bit numbers, the set of all 32 powers of 2
can be perfectly (and minimally) mapped to 0…31
by a multiplication with e.g.
0x04d7651f
giving a 32 bit temporary result
and a logical shift right by 27
which extracts the uppermost 5 bits.
By the way, this constant resembles a
de Bruijn cycle.
Usually finding an optimal constant is difficult.
In absence of a better algorithm one might simply try
several constants and choose the best found;
thousands or even millions of tries are feasible.
As usual a larger choice of nr_slots
typically helps to find better constants
and also gives a better chance to cheaper scrambling functions.
In
Coding multiway branches using customized hash functions
by H.G. Dietz (1992-07)
this theme is applied to switch statements,
although the multiplication was described as being too slow
to be useful (8 cycles at that time);
it also might be that
the mentioned combination of a multiplication and a following shift
was simply overlooked.
It is about time that the tests are repeated.
Considering the age of that document,
it is really a shame that almost no contemporary compiler
makes use of the given results.
We have prepared a document which goes into more detail on this theme.
There are some methods which utilize more than one auxiliary hash function
and lookup into additional arrays to create a perfect hash function.
Bob Jenkins
presents one of the (at runtime) fastest methods
using two auxiliary hash functions
h1 and h2 such as the ones given above
and one small array a:
h(x) = h1(x) ^ a[h2(x)]
Depending on the chosen auxiliary hash functions and context
such a method can often outperform imperfect hashing.
Optionally even a minimal perfect hash function
can be achieved,
i.e. all given numbers are mapped to a contiguous range,
albeit usually resulting in larger tables.
You can download the sources of prototype of a
perfect hashing library.
This is currently an ugly mixture of C and C++
with only rudimentary documentation and tests.
On the other hand it seems to work flawlessly
for up to several thousand entries.
I had an older version already running in a
patch for the LLVM compiler suite.
Unfortunately I can no longer find my patch online.
Also, there has been only little response in the forum;
maybe, some day I will give it another try…
If all actions consist only of assigning a value to a variable, we evidently can replace the structure's jump addresses by the values and replace the jumps by the assignment. We effectively do this in Using a mapping container which also demonstrates possible realizations in C/C++.
 Dispatching on strings in theory
Dispatching on strings in theory
Quite often we want to
interpret strings such as parameters or key words
which means that we need to recognize strings and do the related actions.
I mainly focus on creating dedicated code
dealing with a small to moderate number (up to a few thousand)
of constant strings.
The typical solution is to test a given string to the strings to be recognized one by one which is an else-if chain (an O(n) approach). However there are many ways to create faster code than this:
Perfect hashing seems to be the best approach,
and thus this is the way I will carry further in this chapter.
Perfect hashing can be achieved e.g. by
simple hashing
(for very small sets)
or
Bob Jenkins'
method mentioned
above.
I had good experiences trying both methods in my
perfect hashing library.
In order to prepare a perfect string hash function
you must take at least as much parts (i.e. characters) into account
as are necessary to tell all strings of the set apart,
and it makes sense to take as few as possible.
The string length counts here as one part
and usually is the cheapest element,
provided one does not use null-terminated strings,
however we typically need the length anyway.
Unfortunately selecting the minimal/optimal choice is not easy.
Many authors simply use a function which takes all characters into account.
At least for small sets this seems to be overkill.
The method used by
GPERF
is to select the absolutely necessary ones first,
then add one significant additional part after the other until
the resulting excerpts are unique.
Now that we have a sufficient selection,
all superfluous parts are removed,
and as an additional optimization every pair of chosen parts is tested
whether it can be replaced by a single one.
As far as I can see, the most usable parts are
It makes sense to test the actual length for the occurring minimum length min (or length range min..max) beforehand. Having done this, the first and last min characters can be easily accessed without further length checks. The rare case of an empty string being in the set should be treated specially.
The last method has some charm because is does not need conditional jumps and the extra amount of calculation is moderate (factor and shift are very small constants, and no out-of-bounds access is possible even if the multiplication overflows):
s[(unsigned) ((length-1) * factor) >> shift]
The extracted parts must now be combined to a unique number.
We can just try several
more or less trivial combining functions
(such as a+b, a^b, (a<<3)+b)
until we find a suitable one
which combines the parts but does not give up the "perfectness".
After combining one part after the other in this way
we have the resulting pre-hash value
which can be used as input for an perfect
integer hashing
function.
The resulting hash value can be used as an index for
the string table (for comparison),
and since perfect hashing was achieved,
also for a jump table (switch) or a value table.
It makes sense to split larger string sets by length, i.e. use the length to dispatch to different hash functions. This costs several cycles. However, we then often need much fewer parts and only accesses to constant offsets without range checks; obviously, selecting parts by relative position (type 4) no longer makes sense. The resulting partial perfect hash functions are simpler than one which deals with the whole string set. Each character is read at most twice: One for hashing and one for the final comparison. All in all it may be profitable.
The string table is a concatenation of all partial string tables; an offset to the table index selects the relevant section and the partial hash value the offset within such a section. Optional other tables can be indexed with the same final hash value.
One might try to fill holes within the partial hash value ranges by using them for other partial hash values. In order to faciliate this, it might make sense to use (near) minimal partial perfect hash functions which plant holes at the end of the partial hash value ranges. It helps to place the partial ranges ordered descending by hole count.
If you completely keep apart all length cases (i.e. no hole filling), fixed length comparisons are possible, i.e. you can use cmpmem instead of cmpstr in C, and the comparison loop can even be unrolled (no call) since the length is a constant; for cases with only a single string, it even gets simpler. On the other hand, this complicates the resulting code for a small benefit.
As a matter of fact, GPERF usually produces code which dispatches by length, albeit only one hash function is generated, i.e. the cases are combined thereafter. This is done there by a switch statement with fall-through cases (ordered descending by length) which incrementally create the hash value.
The described method works without problems with all character sets and all bit depths.
If you want to compare strings case insensitively
you could convert all strings to upper or lower case,
i.e. the string to be tested at runtime and the set at compile time.
An often working substitute
(no umlauts or accented characters; possibly false positives)
suitable for ACSII/ANSI/UTF-8/UTF-16 characters
is to convert each part to upper case
by and-ing them with ~0x20
and use a case-insensitive string comparison afterwards.
By cleverly combining the parts you can often save some
ands.
Comparisons of special characters like umlauts or accented characters
are language/region dependent
and should not be handled by the compiler.
Unfortunately hashing is not really suited
to match partial strings
such as prefix or postfix strings.
General pattern matching is even worse.
Prefix strings
can easily be recognized by a decision tree
as these are a special case of string ranges.
Combining trees and hashing is subject to be explored.
The choice of the hash function also might influence the speed of the subsequent string comparison; if e.g. the hash function only returns the first character, the following string comparison will find that the first character matches.
It is worthwhile to calculate whether a perfect hash function derived by the described way is less expensive than a possibly much cheaper non-perfect one using a choice with only very few parts but taking some extra comparisons into account.
Looking at the theme from a different angle
a compiler should (optionally) try to recognize structures
which can be realized by a switch/case construct,
i.e. else-if chains, binary search trees,
nested switch/case statements.
Care should be taken as not to seriously slow down the code
for the cases which are preferred in the original code,
i.e. the cases which were tested first.
As usual the compiler or other tool
should analyze some approaches and choose the best.
Evidently much of the discussion can be applied to other value types as well.
Example: We check for length in range 6..9 and select the character s[(unsigned) ((length-1) * 3) >> 4] (type 4). The resulting value range 70..117 (48 values, range check needed) is compacted into 0..7 (no range check necessary) by
(unsigned) (h * 0x2e5aaa76) >> 29
assuming that unsigned has 32 bit.
| Offset | Length | Choice | Hash | Compacted |
|---|---|---|---|---|
| Monday | 6 | M = 77 | 77 | 7 |
| Tuesday | 7 | u = 117 | 117 | 1 |
| Wednesday | 9 | e = 101 | 101 | 2 |
| Thursday | 8 | h = 104 | 104 | 6 |
| Friday | 6 | F = 70 | 70 | 5 |
| Saturday | 8 | a = 97 | 97 | 4 |
| Sunday | 6 | S = 83 | 83 | 0 |
if (6<=length && length<=9) {
unsigned h = s[(unsigned) ((length-1) * 3) >> 4];
h = (unsigned) (h * 0x2e5aaa76) >> 29;
if (strings[h] == s) { // compare to strings[8]
// Matching string found; now use h to index into table[8]
}
}
Example: We check for length in range 3..9, select the characters s[0] (type 2) and s[length-2] (type 3), and combine them using xor (+ does not work in this case). The combined value could be tested to be in the range 33..56 which are 24 values (range check needed). However we further compact this range into 0..15 (no range check necessary) by
(unsigned) (h * 0x889b53a9) >> 28
| Offset | Length | Choice 1 | Choice 2 | Hash | Compacted |
|---|---|---|---|---|---|
| January | 7 | J = 74 | r = 114 | 56 | 14 |
| February | 8 | F = 70 | r = 114 | 52 | 11 |
| March | 5 | M = 77 | c = 99 | 46 | 8 |
| April | 5 | A = 65 | i = 105 | 40 | 5 |
| May | 3 | M = 77 | a = 97 | 44 | 7 |
| June | 4 | J = 74 | n = 110 | 36 | 3 |
| July | 4 | J = 74 | l = 108 | 38 | 4 |
| August | 6 | A = 65 | s = 115 | 50 | 10 |
| September | 9 | S = 83 | e = 101 | 54 | 13 |
| October | 7 | O = 79 | e = 101 | 42 | 6 |
| November | 8 | N = 78 | e = 101 | 43 | 15 |
| December | 8 | D = 68 | e = 101 | 33 | 9 |
if (3<=length && length<=9) {
unsigned h = (unsigned) s[0] ^ (unsigned) s[length-2];
if (33<=h && h<=56) {
if (strings[h] == s) { // compare to strings[24]
// Matching string found; now use h-33 to index into table[24]
}
}
}
or:
if (3<=length && length<=9) {
unsigned h = (unsigned) s[0] ^ (unsigned) s[length-2];
h -= 33;
if (h <= 56-33) {
if (strings[h] == s) { // compare to strings[24]
// Matching string found; now use h to index into table[24]
}
}
}
or (probably better):
if (3<=length && length<=9) {
unsigned h = (unsigned) s[0] ^ (unsigned) s[length-2];
h = (unsigned) (h * 0x889b53a9) >> 28;
if (strings[h] == s) { // compare to strings[16]
// Matching string found; now use h to index into table[16]
}
}
or even:
unsigned h;
if (((unsigned) (length-3) <= 9-3) &&
(h = (unsigned) s[0] ^ (unsigned) s[length-2],
h = (unsigned) (h * 0x889b53a9) >> 28,
strings[h] == s)) { // compare to strings[16]
// Matching string found; now use h to index into table[16]
}
Example:
We use the same set as above but we split by length.
As we can see,
we have an additional switch which ought to be realized by a
range check and a jump table.
The hole in
the hash value range for length 8
and partial hash value 1
in the string table at offset 9
was reused for the single hash value for length 9.
No range check on the final hash value is necessary
since the table is used up to the last entry.
const string strings[12] = {
// table index length
"May", // 0 = 0 + 0 3
"July", // 1 = 0 + 1 4
"June", // 2 = 1 + 1 4
"April", // 3 = 0 + 3 5
"March", // 4 = 1 + 3 5
"August", // 5 = 0 + 5 6
"January", // 6 = 0 + 6 7
"October", // 7 = 1 + 6 7
"December", // 8 = 0 + 8 8
"September", // 9 = 1 + 8 9 reused hole
"February", // 10 = 2 + 8 8
"November", // 11 = 3 + 8 8
};
// Input: String to be compared (s) and its length (length)
unsigned h;
switch (length) {
case 3:
h = 0 + 0; // 0..0
break;
case 4:
h = ((s[3] >> 2) & 1) + 1; // 1..2
break;
case 5:
h = ((s[0] >> 2) & 1) + 3; // 3..4
break;
case 6:
h = 0 + 5; // 5..5
break;
case 7:
h = ((s[0] >> 2) & 1) + 6; // 6..7
break;
case 8:
h = ((unsigned) (s[0] * 0x2a30f7f4) >> 30) + 8; // 8..11; hole at 1+8
break;
case 9:
h = 0 + 9; // 9..9, reusing a hole
break;
default:
goto string_not_found;
}
if (strings[h] == s) {
// Matching string found; now use h to index into table[12]
}
else {
string_not_found: ;
// Code for non-matching string
}
 Dispatching on strings in reality
Dispatching on strings in realityFree Pascal knows how to dispatch on strings, but Delphi does not, see Speeding up case of string (Pascal).
C and C++ can not dispatch on strings, but with some precompiler magic can be taught to, see Switch on strings (C/C++).
Compilers for .NET 1.x (e.g. C#)
implement a string switch facility
by utilizing a global hash container for
"interned strings".
Since all string constants are interned,
when queried how the given string is interned,
IsInterned
returns null (not interned)
or a unique constant object reference
whose value is fixed and known at least at the first time of executing
the string switch code.
A dispatching on the references follows (ReferenceEquals).
Hence this method effectively resembles the
perfect hash
method.
There is a
German article
about this theme.
Compilers for .NET >= 2.0 (e.g. C#)
do not (necessarily?) depend on
"interned strings"
(CompilerRelaxations.NoStringInterning)
but feature an about equally fast solution.
When the list of cases is short,
an else-if chain is used.
When the list is long enough,
a local hash map is created which maps the string constants
to consecutive numbers.
Hence this method effectively resembles the
hash map container
method.
There is a
German article
about this theme.
Since Java SE 7 one can switch on strings.
In Java string constants are always
"interned"
but the string switch does not really use this feature.
I do not understand why there is no method like
C#'s IsInterned.
The compiler effectively does only some simple minded code transformations, e.g.
switch (s) {
case "abc":
code_1();
break;
case "bde":
code_2();
break;
}
=>
String s_tmp = s;
byte index = -1;
switch (s_tmp.hashCode()) { // lookupswitch, O(log n)
case 96354: // hash code of "abc"
if (s_tmp.equals("abc"))
index = 0;
break;
case 97379: // hash code of "bde"
if (s_tmp.equals("bde"))
index = 1;
break;
}
switch (index) { // tableswitch, O(1); sometimes even lookupswitch
case 0:
code_1();
break;
case 1:
code_2();
break;
}
This is far from optimum! What use is the second switch but to simplify fall-through?! Bizarre!
 Switch on strings (C/C++)
Switch on strings (C/C++)Closely related to the previous chapters Dispatching on strings in theory, and Speeding up case of string (Pascal) is the corresponding implementation in C resp. C++ which simulates a switch statement which dispatches on string constants. Basically I want to enhance the usual else-if structure by supplying a easily readable and manageable substitute ("syntactic sugar") and provide a faster execution as well. I do not want to separate the string constants from their usage as case labels or even duplicate the strings. Unfortunately there seems to be no real alternative to using macros or (even worse) a precompiler.
I will concentrate on the following syntax
where there can be any number of CASE
and one optional DEFAULT at the end.
A C-like break statement is assumed to be implicit
and should be left out.
A continue statement is forbidden!
The macros SWITCH, CASE and DEFAULT
must be placed on different lines.
This SWITCH construct should be nestable.
I have prepared simple test programs
testcase.c / testcase.cpp
which feature the different methods presented here.
SWITCH(selector) CASE(const1) statements CASE(const2) statements … DEFAULT statements END
If multiple CASE should be handled with one statement list, you can use a goto statement or the following macro sequence which is allowed to be placed on one line:
CASE_MULTI(const1) CASE_OR(const2) CASE_OR(const3) … CASE_DO statements
Nothing else but CASE_OR is allowed between
CASE_MULTI(const) and CASE_DO.
CASE_MULTI(const) can be replaced by
CASE_MULTI0 CASE_OR(const).
The built-in preprocessor of C / C++ can not do all of the
needed magic of directly creating a program transformation
such as the one I have manually done above for Pascal
without introducing a considerable amount of overhead
and/or limitations on usability,
however we can come quite close.
See
case_ifc.c
and
case_ifs.cpp
for a trivial else-if implementation.
If we select a hash function which creates disjunct values
for all given strings of a switch statement,
we can directly dispatch on the hash value with an
integer switch statement
and just add one if per case.
We might utilize the C++0x feature constexpr
to calculate a manifest hash constant from a string constant
since unfortunately a simple macro is not sufficient.
We could however calculate the hash constant manually …
But do you really want to manage that?
The resulting code typically has to deal
with a large sparsely filled number range
which inhibits a jump table;
the best the compiler can do is to use a tree-like jump cascade
or possibly use hashing (once more) too.
The main problem here is that you have to guarantee
that the hash values are disjunct, i.e. that there are no conflicts;
this situation is called a perfect hash.
Fortunately the compiler complains if this condition is not fulfilled;
in this case you must choose a different hash function.
If you have several hash functions you have to pay attention
that you use the same one for all case expressions
of one switch.
See
case_ce.cpp.
We can collect the string constants during the first run
during runtime over the simulated switch statement
and use the map created that way in all subsequent runs
to feed an integer switch statement.
This is possible by using a static local variable.
One problem I see here is to let the compiler generate indexes
which span a tight enough number range
to allow and suggest the compiler to create a jump table.
Obviously we could supply the indexes manually but this is
inelegant, error-prone and tedious.
Unfortunately the macro processor is too stupid to enable the creation of
an incrementing macro which can be used from within an other macro.
See the free
boost library
for the effort it takes to even create a counting facility
using an include file in
boost/preprocessor/slot/counter.hpp.
The macro stuff of e.g.
NASM
does not pose such problems…
As a poor substitute we might use __LINE__
and have to bite some bullets:
The numbers do not start at 0 (we can compensate this),
we must have each CASE on a different line,
and we will get holes in the number range
if we do not put each CASE in a single line.
Almost always however this approach is good enough to get the job done.
BTW: Should Microsoft's MVS complain that __LINE__ is not constant,
according to a
forum post
you should change the compiler setting from
"Program Database for Edit and Continue" to "Program Database".
Bizarre!
See
case_hm.cpp
for a solution using an STL container.
The interesting part of this approach is that
- once we have gathered all string constants -
we can put some effort in optimizing the mapping algorithm
by selecting the best available
(i.e. fastest and eventually perfect) hash function
or even by using a completely different mapping algorithm.
This is possible and makes sense because it will be evaluated
at most once per program run and
the effort typically is amortized in subsequent executions of the
SWITCH, provided that the SWITCH is executed often enough.
By doing this we can easily outperform the solution which uses the STL container.
Some precautions should be taken to
protect this first pass from being executed simultaneously multiple times
in a multi-threaded program, see
Singletons / Do once only.
The load factor α of the hash container currently is
0.5…1.0 (50%…100%)
which I think is a reasonable choice.
For a perfectly randomizing hash function
the number of expected string comparisons is about 1+α/2,
and thus 1.25…1.5.
See
case_map.c / case_map.cpp
for a self-made container featuring a hash optimizer.
The variant
case_ms.cpp
uses STL strings instead of 0 terminated character arrays.
This can improve most hash functions since the string lengths
are very "cheap" to access;
also more very simple hash functions can be created
where e.g. the length itself and/or the last character(s) are used.
Unfortunately we can not really expect that a compiler can optimize all the things of the first pass we now do at runtime into a static structure containing the optimized hash map and that the call to the selected hash function becomes static or even inlined…
We also could abandon with the integer switch statement
as the implementation base completely by
putting the statements of the CASE bodies
directly into the mapping container
using the C++0x feature lambda.
This is very similar to the approach above.
The
boost library
defines such a construct in
boost\lambda\switch.hpp.
Here you can find another
implementation
using a similar variant.
The approach theoretically looks nice on first sight
but I was disappointed when I saw the resulting code.
Also each body is a separate function thereby forbidding
the goto statements mentioned above needed to pipe multiple
cases into one statement list.
For these reasons I will not carry this further.
Similarly as for
Pascal
using a precompiler could also be a solution to problems like this
but being forced to always apply an extra compilation step is probably overkill.
The kludge using a
self-made hash container
given by
case_map.c / case_map.cpp / case_ms.cpp
is a reasonable solution to the string switch problem.
All the overhead performed during runtime
including eventually needed locking mechanisms
could easily be eliminated and done at compile time instead,
if string-switches were a built-in language feature.
Unfortunately C/C++ does not even sport properly implemented strings…